eFatigue gives you everything you need to perform state-of-the-art fatigue analysis over the web. Click here to learn more about eFatigue.
Finite Element Model Stress-Life Technical Background
In order to accurately assess fatigue lives from finite element models consideration must be given to multiaixal stresses, stress gradients and variable amplitude out-of-phase loading in addition to traditional factors such as surface finish and mean stresses.
Almost all fatigue data are reported in terms of tensile stress for constant amplitude uniaxial loading, i.e. the SN or εN material curves. But, the state of stress and strain are usually multiaxial in any structure or component. A multiaxial fatigue analysis is needed to relate the more complex stress state found in all structures and components to the simple stress state used for material testing. What stress, or strain, should be used as the basis of comparison, principle, shear or von Mises equivalent? Fatigue crack nucleation and early growth is a process that is driven by shear stresses. Once nucleated, a crack tends to grow in perpendicular to the maximum principle stress direction. As a result, two fatigue damage models must always be used to accurately assess fatigue lives. One that considers the possibility of shear stress/strain dominated failures and a second one that considers principle stress/strain failure mechanisms.
Stress and strain gradient effects also play an important role in accurately assessing fatigue damage. Small notch or stress concentration features or geometries with high stress gradients are less effective in fatigue than larger features or smaller gradients with the same maximum stress. In conventional fatigue analysis, the stress gradient effect is taken into account by using a fatigue notch factor, Kf, rather than the stress concentration factor Kt. In practice Kf < Kt. Since there is no concept of a Kt or nominal stress in a finite element model stress gradient effects are considered directly. In conventional fatigue analysis, Kt gives the stress on the surface and Kf gives a lower stress just below the surface. In a finite element model it is easy to compute the stress at any distance below the surface. Typically this distance is 0.5 mm. The method is described in the literature as the critical distance method.
Performing a variable amplitude multiaxial fatigue analysis with stress gradient effects on every node or element is too time consuming to be practical. Methods have been devised to screen out those elements and nodes with little or no fatigue damage. Fatigue is a surface phenomena where fatigue cracks start. Only those nodes and elements on the surface are considered substantially reducing the number of nodes to be analyzed. Next those nodes and elements with stresses too small to cause any fatigue damage are eliminated. The result of this screening is a manageable number of nodes and elements, each of which is treated as a potential variable amplitude multiaxial fatigue problem.
Theories
Theories and equations employed in the eFatigue FEM Stress-Life Analyzer are described in this section. A description of the input and output options are given in the next section.
Multiaxial Fatigue Models
Two damage models are used in the eFatigue FEM Stress-Life Analyzer. The Findley model considers shear dominated failures and the Goodman model considers tensile dominated failures.
Findley
Findley, W. N., "A Theory for the Effect of Mean Stress on Fatigue of Metals Under Combined Torsion and Axial Load or Bending," Journal of Engineering for Industry, Nov. 1959, 301-306
Findley reviewed the experimental data and suggested that the normal stress σn, acting on a shear plane will influence the allowable alternating shear stress, Δτ/2.
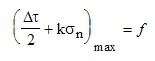
Parabolic forms were investigated but Findley concluded that the linear form was sufficient to describe the experimental data. Here k is a material constant that is related to the materials' sensitivity to normal stresses and f is directly related to the materials' fatigue strength. For ductile materials, k typically varies between 0.2 and 0.3.
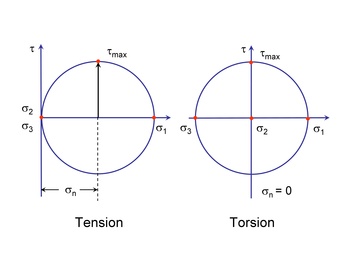
Mohr's circle for both tension and torsion are show below. Both loading conditions have the same shear stress. In an R= -1 fatigue test, both tension and torsion loading will have the same shear stress range acting on a small microcrack located on the maximum shear stress plane. Mohr's circle shows that tension loading will also have a normal stress cycle with the same range as the shear stress acting on this shear plane. This will result in a higher value of the damage parameter for tension loading. The result is that for the same shear stress range, tension loading will always be more damaging than torsion.
Findley's model differs from other yield criteria models in that it identifies the stress acting on a specific plane within the material. These are termed critical planes and can be defined as one or more planes within a material subject to a maximum value of a damage criterion. Fatigue life is controlled by the combination of stresses and strains acting on a critical plane. Findley identifies a critical plane for fatigue crack initiation and growth that is dependent on both alternating shear stress and maximum normal stress. The combined action of shear and normal stresses is responsible for fatigue damage and the maximum value of the quantity in parentheses is used rather than the maximum value of shear stress. This concept is easily illustrated for torsion loading. The stresses σθ and τθ on a plane oriented at an angle θ can be computed from the applied shear stress τxy. Values of τθ + kσθ for a value of 0.3 are plotted below and failure is expected to occur on the plane that has the largest combination of Δτ/2 + kσn.
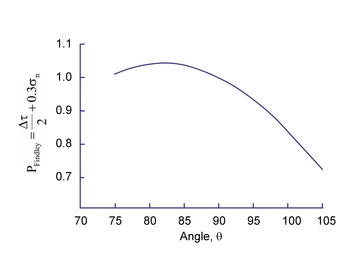
The maximum value of the parameter occurs at angles of about 82° and -8°.
The Findley criterion is often applied for the case of finite long-life fatigue. An equation of the form
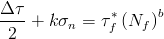
is used to compute fatigue lives. In this equation, tf* is computed from the torsional fatigue strength coefficient, tf', using
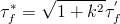
The correction factor
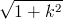 is small and typically has a value of only about 1.04.
is small and typically has a value of only about 1.04.
In complex multiaxial loading, the maximum fatigue damage may not be caused by the maximum stress range.
Rather, the maximum damage is caused by the combined effects of shear stress range and normal stress.
The normal stress term in
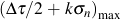 combines state of stress and mean stress effects in single term.
combines state of stress and mean stress effects in single term.
Goodman
Tensile mean stresses are known to reduce the fatigue strength of a component. Compressive mean stresses increase the performance and are frequently used to increase the fatigue strength of a manufactured part. The most common method for accounting for mean stresses is the Goodman Diagram. It was first proposed in 1890. Goodman writes ".. whether the assumptions of the theory are justifiable or not.... We adopt it simply because it is the easiest to use, and for all practical purposes, represents Wöhlers data." The fatigue limit for zero mean stress is plotted on one axis and the ultimate strength on the other.
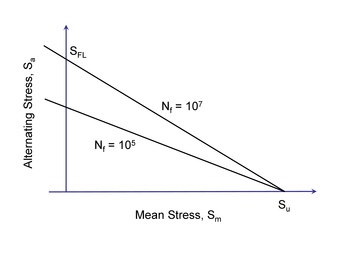
For finite lives, an equivalent completely reversed stress, Seq, is computed from the stress amplitude, Sa, mean stress, Sm , and ultimate strength, Su, and then compared with the material SN curve.
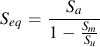
The traditional Goodman diagram can be used with the principal stresses to evaluate fatigue under multiaxial loading. Care must be taken when using principal stresses for loading which involves both tension and compression. The principal stresses and their directions are shown below for both tension and compression loading.
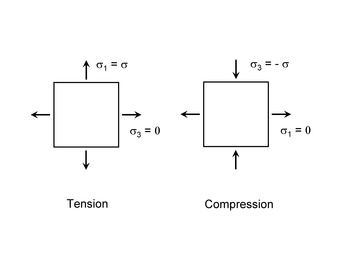
By convention, the principal stresses are always ordered so that σ1 >= σ2 >= σ3. Note that during a simple tension compression loading the principal stress direction rotates 90°. To avoid these problems, the normal tensile stresses are computed for a plane or direction and the range of normal stress acting on this plane is used as the stress range and combined with the mean stress acting on the same plane to calculate the fatigue lives. Just as with the Findley model in complex multiaxial loading, the highest combination of normal stress range and mean stress will produce the most fatigue damage.
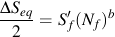
Go to the Multiaxial Technical Background section for a more complete description of the material properties and fatigue analysis.
Surface Finish Effects
Materials, as they are tested, are always in a different surface condition than the materials as they are actually used. Test specimens are polished to eliminate the effects of surface finish. Fatigue cracks usually nucleate on the surface so that the condition of the surface plays a major role in the fatigue resistance of a component, but only at long lives. At short lives cyclic plasticity dominates the behavior of the material and surface finish is less important. The degree of surface damage depends not only on the processing but also on the strength of the material. Higher strength materials are more susceptible to surface damage. An important part of the analysis is to "correct" the basic materials data to obtain an estimate of the fatigue life of the material in the component or structure of interest. To account for this in the analysis the material fatigue limit is reduced by a surface finish factor, kSF.
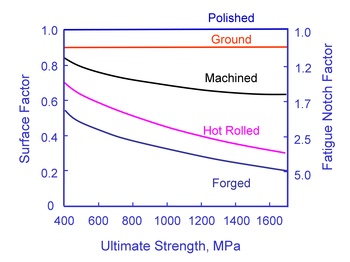
The original data for constructing this curve is shown below. The factors tend to provide conservative estimates for fatigue lives.
(From Noll and Lipson, "Allowable Working Stresses", Society for Experimental Stress Analysis, Vol. III, no. 2, 1949)
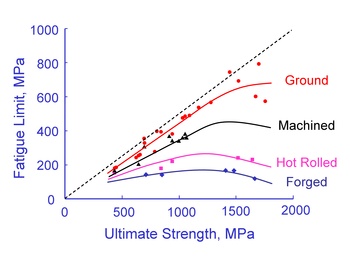
These data are fit to a simple power function to obtain an estimate of the surface factor for any hardness steel.
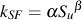
| α | β | |
| Ground | 1.58 | -0.085 |
| Machined | 4.51 | -0.265 |
| Hot Rolled | 57.7 | -0.718 |
| Forged | 272 | -0.995 |
The effect of surface finish is reduced for higher strain levels where cyclic plasticity controls the behavior. Surface finish won't have any effect on the static strength of the material ( 1 cycle ).
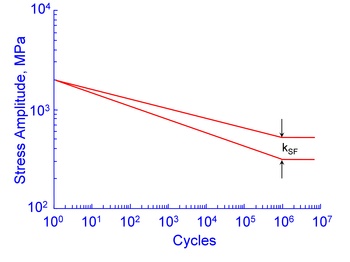
Surface finish effects are included in the analysis by altering the slope of the stress-life curve. The surface finish corrected slope is given by
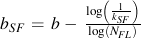
Stress Gradient Effects
Small stress concentration features or geometries with high stress gradients are less effective in fatigue than larger features or smaller gradients with the same maximum stress. A plate with a small hole, say 0.1mm, will have a much longer fatigue life than one with a large hole of 10mm even though both plates have the same stress concentration factor and maximum stress. In conventional fatigue analysis, the stress gradient effect is taken into account by using a emperical fatigue notch factor, Kf, rather than the stress concentration factor Kt. Since there is no concept of a Kt or nominal stress in a finite element model stress gradient effects are considered directly. The figure below shows the stress distribution in a plate for three different hole sizes. All of the holes have the same maximum stress, three times the nominal stress.
The figure shows that the stresses are independent of size only at the edge of the hole and very far from the hole. The dashed line in the figure is drawn at 0.5mm. Here the stresses increase as the size of the hole increases. Suppose crack nucleation mechanisms result in a crack with a size of 0.5mm. For the smallest hole, 0.1mm, the stress available for continued growth is only 100MPa, the nominal stress. The same size crack is subjected to a stress of 275 MPa in the larger hole, nearly equal to the maximum stress.
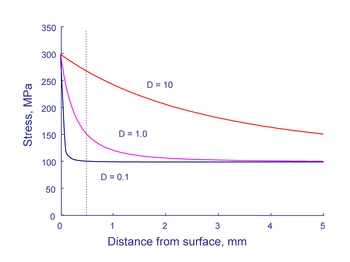
What about the nucleation of a crack around a hole of different sizes? It is useful to think about a process zone for crack nucleation. Materials are not continuous and homogeneous on the size scale that crack nucleation mechanisms operate. The grain size of the material is a convienient way to visualize the fatigue process zone. The figure below shows the grain size superimposed on the stress distribution from the figure above. What is the stress in the process zone? A simple first approximation would be to take the stress in the center of the grain. Thus, a stress of 275MPa would be used to compute the fatigue life of a 10mm hole and a stress of 100MPa would be used for the 0.1mm hole.
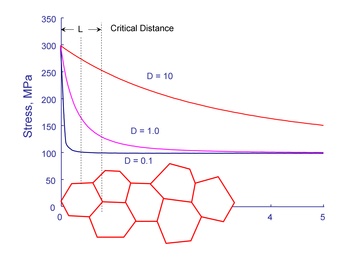
The modern view of fatigue is that when a material is stressed at the fatigue limit a microcrack will form but not grow outside of the process zone. Stresses gradient effects are included in the fatigue analysis in a very simple and straightforward manner. Stresses and strains at a distance L/2 from the surface are used rather than the surface stresses and strains.
The critical distance can be expressed in terms of the threshold stress intensity, ΔKTH, and fatigue limit range, ΔσFL, as
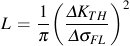
Computing the critical distance from the threshold stress intensity is difficult because the threshold stress intensity, particularly for small microcracks, is usually unknown. Fortunately there is a good direct correlation between the critical distance and fatigue limit.
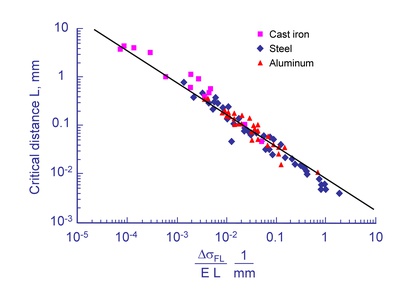
From: Atzori, Meneghetti and Susmel, "Material fatigue properties for assessing mechanical components weakened by notches and defects" Fatigue and fracture of Engineering Materials and Structures, Vol. 28, 83-97, 2005
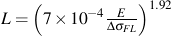
Variable Amplitude
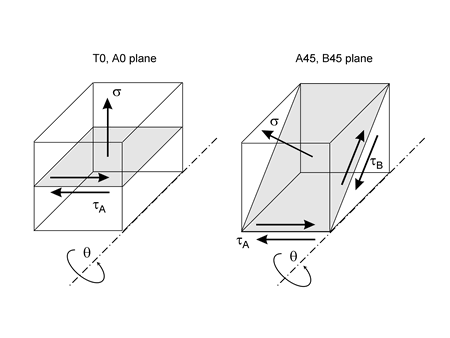
A common feature of many multiaxial fatigue criteria is that they are expressed as a general form that includes both stress amplitude and normal stress during a loading cycle. Multiaxial fatigue models differ in the interpretation of how the stress amplitude and normal stress are defined. Unfortunately, except for very simple load cases, there are no analytical solutions to determine the most damaging combination of stress amplitude and normal stress. All possible failure planes must be considered. This requires an efficient algorithm.Fatigue cracks begin on or near the surface. On the surface the stress state is one of plane stress so that there are only three stress components σx, σy and τxy. All other stressses are zero. For these stress states, the accumulation of fatigue damage that will eventually lead to fatigue cracks will occur on planes that are oriented either 45° or 90° to the free surface. Cracks can nucleate an any angle θ on the surface. There are four possible damage systems shown in the figure below: T0, tensile stresses acting on a plane perpendicular to the free surface, A0 shear stresses acting on a plane perpendicular to the free surface, A45 in-plane shear stresses acting on a 45° plane, and B45 out-of-plane shear stresses acting on a 45° plane.
Fatigue damage is computed in 10° increments to find the maximum damage.
At this time the eFatigue FEM Stress_Life Analyzer does not do any cycle counting.
Input and Output Description
This section gives a description of the input and output options for the eFatigue FEM Stress-Life Analyzer.
Loading
The first step in the process is to select a finite element model for the computation. You can upload a new file from your computer or select from a list of previously uploaded files.

Uploading is a two stage process. First, the file is uploaded to your working directory in eFatigue. You can change your working directory by going to Files in the left sidebar. Once the file is uploaded it is then validated. The validation process consists of reading the entire file to to make sure that it can be read by eFatigue and that it contains all of the information required by the analysis. A list of surface nodes and elements is constructed and linked with the original file. The validation process is only preformed once on each file.
You can also select a model from a list of previously validated files. Clicking on the File Finder will present a list of valid finite element models in your working directory.

Next the units for the model must be selected.
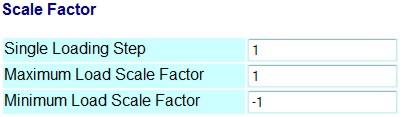
Many finite element models contain only one load step. Fatigue requires cyclic loading. This is acomplished by defining a scale factor for the maximum and minimum load. For example, loads that cycle between zero and the maximum load would have scale factors of Maximum Load Scale Factor = 1 and Minimum Load Scale Factor = 0. Data is scaled as follows: Stress range = ( finite element model stress ) * ( Maximum Load Scale Factor - Minimum Load Scale Factor ) If the model contains several load cases, you can select any one of them for analysis.

Material
At a minimum, the ultimate strength must be entered for the material of interest. You can also use the Material Property Finder to help you select a material. Frequently the multiaxial fatigue material properties needed for the analysis are not available. eFatigue will make an estimate of these properties.
eFatigue uses the following rules for estimating material properties.
Elastic Properties
Estimated:
| Elastic Modulus, E |
207,000 MPa for Steel 80,000 MPa for Aluminum |
| Poisson's Ratio, ν | 0.3 |
| Shear Modulus, G | 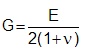 |
Tensile Stress Life Curve
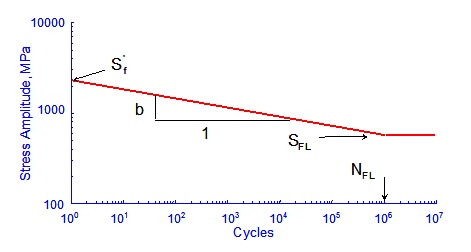
The stress life curve is described by four properties; fatigue limit, SFL, fatigue limit cycles, NFL, intercept at 1 cycle, Sf', and slope, b. Various approximations are made depending on which material properties are specified.
Four properties specified
Only three of these properties are independent. If all four are specified, the fatigue limit is ignored and recalculated to be consistent with the other properties.
Three properties specified
When any three properties are known, the remaining one is calculated directly.
Two properties specified
A default value of NFL =106 cycles is assumed if the slope and intercept is specified. The fatigue limit is then computed.
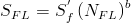
A default slope of -0.085 is assumed when only the fatigue limit and fatigue limit cycles is specified. The intercept is then computed.
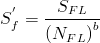
One property specified
A default value of NFL = 106 is assumed. When either the fatigue limit or stress life intercept is entered, a slope of -0.085 is assumed and the other property is calculated.
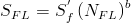
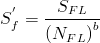
No property specified
Lacking other data, these constants are estimated from the Ultimate Strength, Su.
| Stress Life Intercept, Sf' | Sf' = 1.62 Su |
| Fatigue Limit, SFL | SFL = 0.5 Su |
| Stress Life Slope, b | 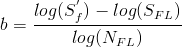 |
| Fatigue Limit Cycles, NFL | NFL = 106 |
Torsion Stress Life Curve
Torsion stress life curves can be formulated in terms either maximum shear stress or octahedral shear stress. First, any properties that are specified are used. Lacking test data, these properties are estimated from the tensile stress life curve constants that have been determined above.
Fatigue limit cycles, NFL, is assumed to be the same for both tension and shear, and a separate property is not defined.
Maximum Shear Stress
Findley's model is assumed to be valid for converting tensile data into maximum shear stress data. The ratio of shear to tensile properties depends on the constant k in Findley's model.
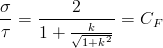
This correction factor, CF, typically varies from 1.2 to 1.5
| Maximum Shear Intercept, Tf'max | Tf'max = Sf' / CF |
| Maximum Shear Slope, bmax | bmax = b |
| Maximum Shear Fatigue Limit, TFLmax | TFLmax = SFL / CF |
Findley Model Constants
The Findley constant, k, is computed from the ratio of tensile and shear fatigue limits when these properties are specified.
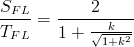
In the absence of test data, a default value of 0.3 is assumed.
Surface Finish
You can enter a surface finish factor directly or select the type of surface from the list. Leaving this field blank will result in a default surface finish factor of 1.

Stress Gradient
Stress gradient effects can be disabled by selecting off. In this case fatigue lives will be computed from the surface stresses.

When stress gradient effects are enabled, which is recommended for the best fatigue estimates, the critical distance may be entered directly. Otherwise it will be estimated from the following equation:
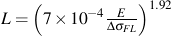
Output Definition
Results of the analysis will be stored in your working directory. This includes all plots and numerical results. You can select your own file name or use the default.

Quick look plots are created for up to 10 nodes after the analysis is completed. These show the sensitivity of the fatigue life at the node to mean stress, material strength, loading and surface finish. You can either leave the list of nodes blank and the most damaging 10 nodes will be plotted or you can specify up to 10 nodes of interest. If you specify more than 10 nodes only the first 10 will be plotted.
A list can be defined using the - range identifier, nodes should be separated by a space. e.g. 1-5 17

eFatigue creates output files in the same format as the input file of fatigue lives or safety factors that can be displayed as contour plots in your FEA viewer. This file will be written to your working directory using the root file name from the input file. You can download this file when the analysis finishes by right clicking on the file name in your working directory. This can be disabled by selecting None from the list.

Analysis Results
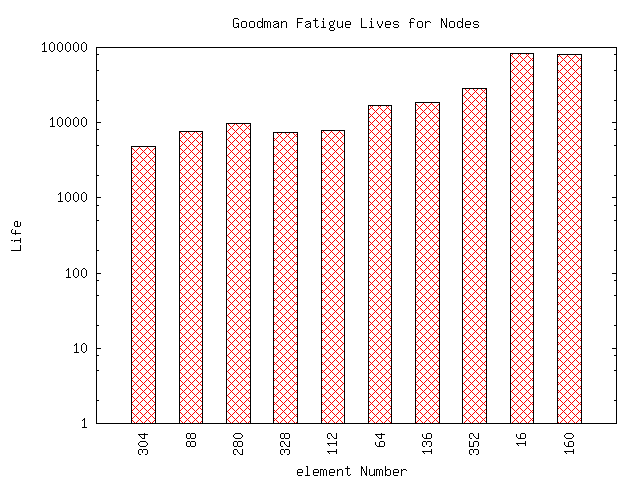
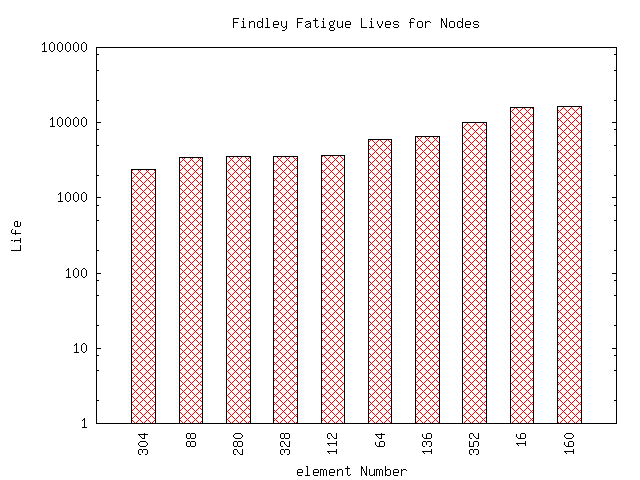
Results from the eFatigue Stress-Life Analyzer are presented in a series of tables and graphs. The minimum fatigue life is given for both Goodman and Findley models. The expected life is the minimum of the two models.

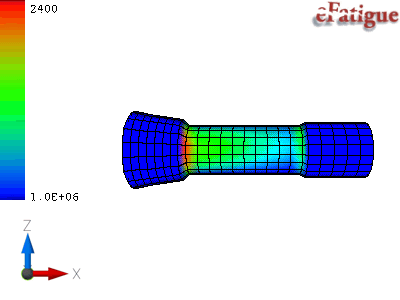
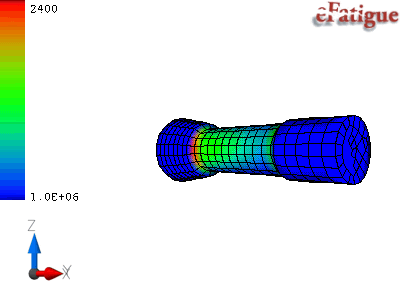
Contour plots of fatigue lives or safety factors are automatically produced to show the area where fatigue failures are expected.
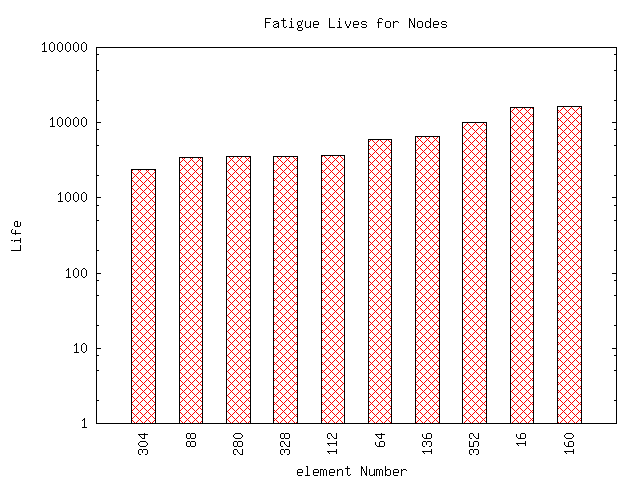
Next a bar chart of the fatigue lives for the 10 worst nodes, or the 10 nodes you selected, are given. This chart is based on the minimum of the two fatigue models.
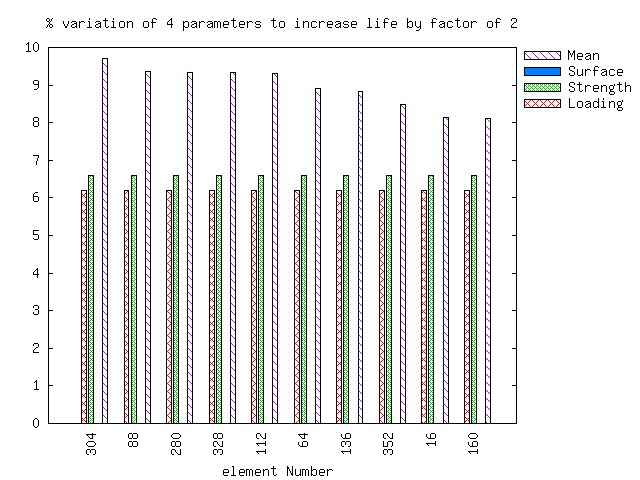
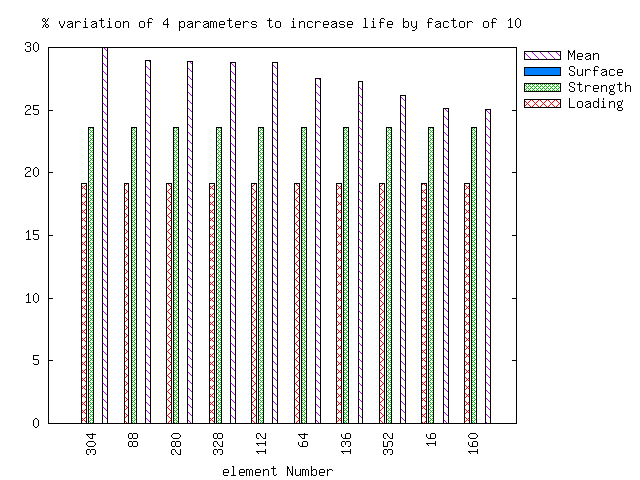
A sensitivity study of the fatigue life on the input variables is then given. The first chart shows how much you would have to change the input variables to get a factor of 2 increase in fatigue life. The second chart gives the same information for a factor of 10. Surface finish factor is often omitted from these charts because you can not change it enough to obtain an increase in life. For example, you can not improve on a surface finish factor that already has a value of 1.
A chart showing the biaxial stress ratio, σ3/σ1 for the critical nodes is given. Uniaxial loading has a value of 0. Torsion is -1 and biaxial tension is 1.
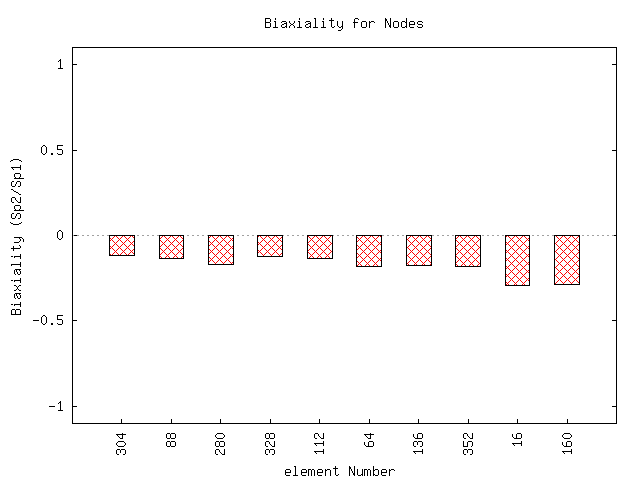
The next two charts give the results of the individual fatigue models.
Finally, a listing of the input variables used in the analysis is presented