eFatigue gives you everything you need to perform state-of-the-art fatigue analysis over the web. Click here to learn more about eFatigue.

Probabilistic Stress-Life Technical Background

Stress life analysis can be summarized as a series of steps:

• define applied stress range
• compute equivalent stress to account for mean stresses
• select material properties
• correct material properties for surface finish and loading effects
• determine stress concentration factor
• compute fatigue notch factor for size effects
• solve the equations

Go to the Constant Amplitude Technical Background section for a more complete description of the fatigue variables.

Mathematically, stress life involves solving the following relationship to obtain the fatigue life N_f.

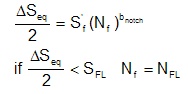
The slope b_notch is a function of other variables and is computed as follows:

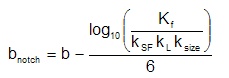
Variability in the material SN slope b, fatigue notch factor K_f, and surface finish, k_SF are included in the analysis. No variability in the loading factor, k_L or size factor k_size is considered because this variability is much smaller than the others.

The Goodman mean stress correction is employed to obtain an equivalent stress, ΔS_eq. It is computed from the stresses that are entered and the ultimate strength S_u.

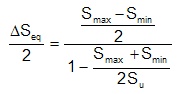
Monte Carlo simulation is employed to obtain several estimates of the fatigue life. These variables, ΔS_eq, S_f' and b_notch, are sampled or computed from their underlying statistical distributions and the fatigue life is calculated. Variability in ΔS_eq is computed from the variability in S_max, S_min or S_a, S_mean and S_u. Similarly, variability in b_notch is computed from variability in K_f, k_SF and b. This process is repeated 1000 times to obtain an estimate of the failure probability. The number of simulations is increased to 10,000 when the probability of failure is small.

Loading Variability

Statistical distributions can be specified for any of the loading variables. These loading variables are assumed to be statistically independent. Typically there is a strong correlation between these variables. For example, measured strains from a vibrating bracket are shown below. High tension strains are often followed by high compressive strains.

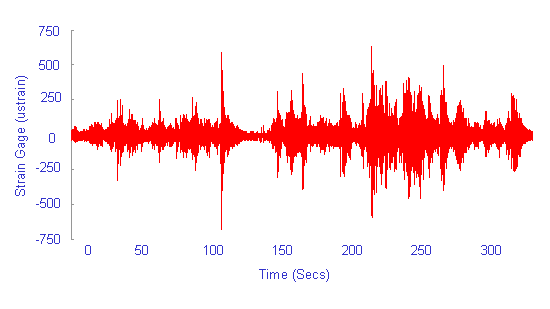
For loading simulations like this it is better to enter alternating stress and mean than maximum and minimum stresses.

Reasonable values for the minimum and mean stress include zero. This creates a problem in computing the standard deviation from the COV. Whenever either of these variables is zero, enter the standard deviation as the scale factor. Only Normal and Uniform distributions can be used with a zero value.

What is a reasonable variability for the loading variables? Naturally every situation is different but based on past experience we can provide some general guidance. The relationship between standard deviation and COV for a LogNormal distribution is given below. Three standard deviations represent most (99.7%) of the data. Most of the data is within ±16% of the median for a COV of 0.05 and within a factor of ±2 for a COV of 0.25.

When comparing loading histories for determining the variability it is convenient to define an equivalent constant amplitude load from a variable amplitude history. That is, what constant amplitude load would produce the same fatigue life as the original loading history? The equivalent load, F_eq for 10⁶ constant amplitude cycles can be computed from the loading history as

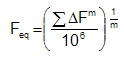
where m is the slope of the SN curve. Typically this should be 4 - 6 for notched components. Two sets of data are plotted in the figure below. One set of data comes from test track driving of a motor home, the other comes from driving an auto in various cities during normal operation.

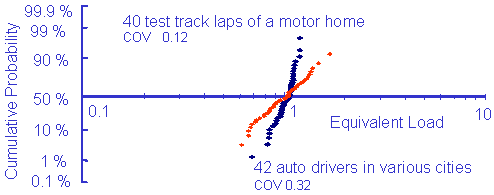
Here we are interested in the COV for the two sets of data. The test track data has a COV of 0.12 which is typical of controlled processes. Unsupervised city driving has much more variability with a COV of 0.3.

Selecting an appropriate variability will depend on how well controlled the loading will be. Many customers with widely varying usage characteristics will have a high variability.

Materials

Statistical distributions may be specified for any of the material properties. Selecting None for the distribution will result in a constant value in the calculations. The ultimate strength, S_u must be specified.

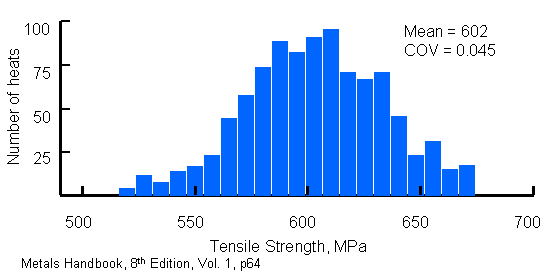
Normal and LogNormal distributions are most frequently used for strength data. Test data from Metals Handbook, 8th Edition, Vol. 1, p64 is shown below. These are typical and reasonable values for the COV range from 0.05 to 0.10.

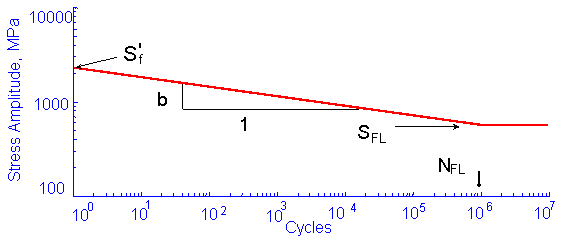
The stress life curve is described by four properties; fatigue limit, S_FL, fatigue limit cycles, N_FL, intercept at 1 cycle S_f' and slope, b.

Statistical distributions may be used with both entered and default material properties. The distributions for each material property will depend on which properties are entered and those that are default values.

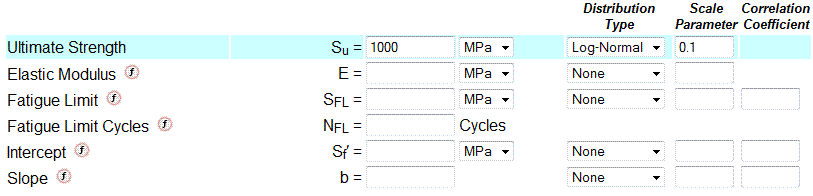
Default values for statistical parameters will be the same as the defaults for the material properties. For example, entering only the Ultimate Strength without entering the other properties will be the same as defining the properties as follows:

Specified statistical distributions will be ignored for any parameter not entered and default statistical parameters will be used in the analysis.

The fatigue limit and slope are correlated to the intercept. The intercept is correlated to the ultimate strength.

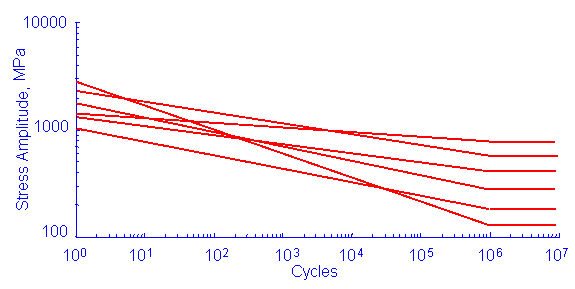
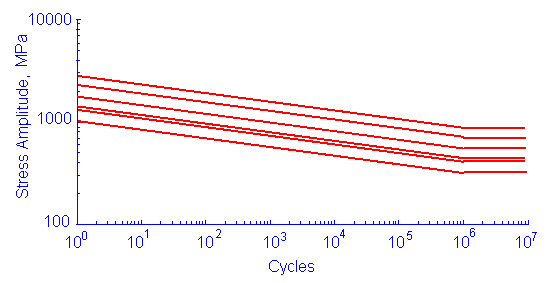
In this example, all of the SN material properties, S_FL, S_f', and b have statistical distributions. There is no correlation between any of the input variables and a series of SN curves will be generated similar to those shown below. Only two of these properties are independent. If all three are specified, the values specified for the slope are ignored and recalculated to be consistent with the fatigue limit and intercept.

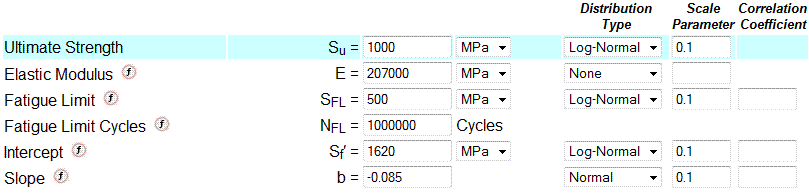
The simulated variability shown below is unrealistically large. The fatigue constants describing the material are not independent variables. There is a strong negative correlation between the slope and intercept. High values of the intercept tend to have corresponding small values of the slope. A better simulation will occur if the slope and the intercept are treated as correlated variables.

By specifying the correlation coefficient between the slope and intercept the slope will be small when the intercept is large giving a much more realistic material simulation.

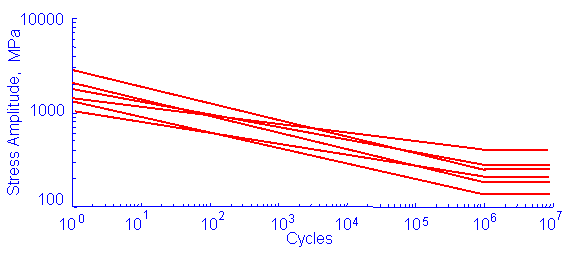
Realistic simulations can also be obtained by assuming the slope to be constant and all of the variability being in the intercept.

There is also an observed correlation between the material strength and fatigue limit and intercept. Materials with high static strengths also have high fatigue strengths. Specifying a correlation coefficient for the intercept and/or fatigue strength will correlate it with the ultimate strength.

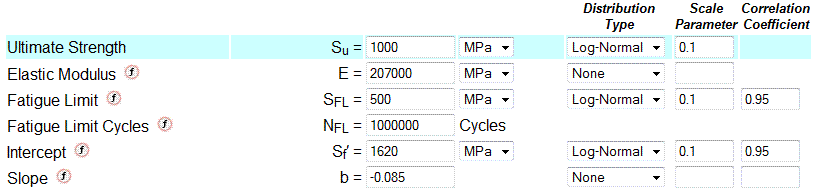
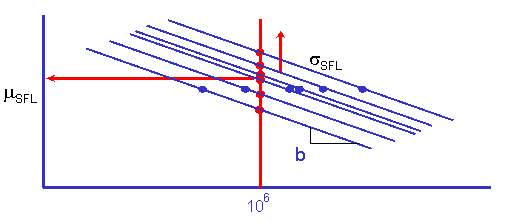
It is not possible to directly measure the variability in fatigue properties because a constant life test can not be conducted. Fatigue strength variability is inferred from the variability in fatigue lives and the slope of the materials SN curve.

The following data from Sinclair and Dolan for 7075-T6 aluminum has a COV of 1.39 in fatigue life. This can be converted into a variability in fatigue strength by this process:

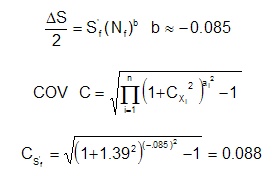
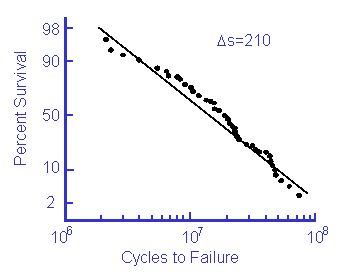
In the absence of test data, a COV = 0.1 would be a reasonable assumption.

The loading and size factors are geometric variables and the expected variability is expected to be much smaller than the other variabilities and can be ignored. Statistical distributions are only permitted for the surface finish. Surface finish data from an aluminum casting is given below.

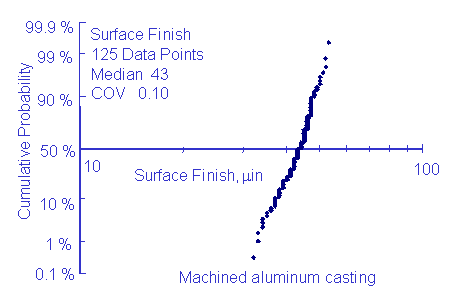
Shigley recommends COV's ranging from 0.06 to 0.13 depending on the process.

Stress Concentration

Fatigue notch factors are computed from the stress concentration factors so that the fatigue notch factor will have the same distribution as the stress concentration factor. The variability in stress concentrations will depend on the application. For example, the variability in the stress concentration for a drilled hole will be very small. Here we may estimate a COV = 0.05. The variability in a welded joint will be much higher where COV's of 0.2 or 0.3 would be appropriate.

The Simulation

Typically 100 trials are used in the simulation resulting in 100 calculated fatigue lives. When the equivalent stress is less than the fatigue limit, the life is set equal to the fatigue limit cycles. The number of lives less than the fatigue limit cycles is probability of failure. If the probability of failure is less than 5%, the number of simulations is increased to 1000 to obtain a more accurate number.

Output Results

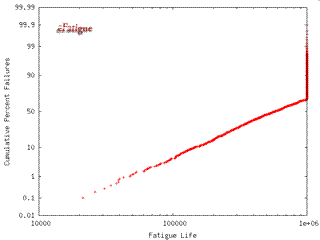
Results of the simulation are given in graphical and tabular formats. First, the median life from the simulation is given. If the fatigue lives in the simulation are finite, a cumulative distribution of the calculated lives is presented in a LogNormal format. This chart is useful for determining probabilities of failure for other lives. Numerical values for this plot are available as the log of the life and number of standard deviations.

A probabilistic sensitivity analysis is performed to determine which variables have the highest contribution to the variability in fatigue lives. The probabilistic sensitivity factor α_i is determined as:

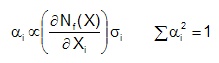
The first term ∂N_f(X) / ∂X_i is the influence of the variable X_i on the fatigue life. This determines the most important variables affecting the fatigue life. It is multiplied by the standard deviation σ_i. A variable that may have a large influence on the fatigue life may have very little variability so that it will not contribute to the variability in fatigue lives. The elastic modulus is an example of such a variable. Results are plotted in a pie chart.

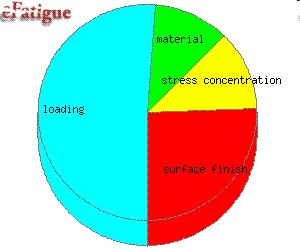
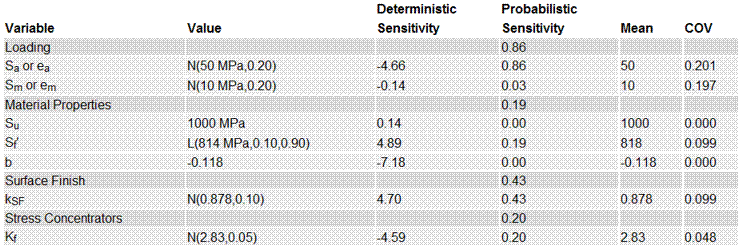
A table of the sensitivity factors is given. Mean and COV of the distributions used in the simulation are shown in the right side of the table.

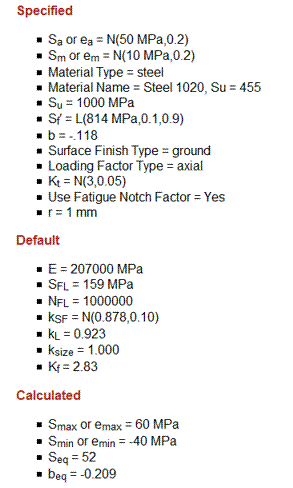
A table of results from the simulation is also given. The input data is displayed first. All calculated variables are also given.