
eFatigue gives you everything you need to perform state-of-the-art fatigue analysis over the web. Click here to learn more about eFatigue.
Strain-Life for Welds Technical Background
Strain life analysis can be summarized as a series of steps:
- define applied nominal stress or strain range
- select material properties
- choose a residual stress
- determine stress concentration factor
- use Neuber's rule to compute local stresses and strains
- solve the equations
Two steps have been added to the constant amplitude strain life annalysis to accomodate welded structures. First residual stresses from the welding process must be considered. An effective stress concentration factor is then determined from the macroscopic geometry of the weld and material strength.
Go to the Constant Amplitude Technical Background section for a more complete description of the fatigue variables and strain life analysis.
Residual Stress
Residual stresses from the welding process can have a significant influence on the fatigue resistance of a welded structure. A local tensile residual stress is produced at the weld toe when the weld metal solidifies. Additional residual stresses due to weld distorsions may also be present. A common assumption is that the residual stress in the as welded condition will be equal to the yield strength of the material. This is the default value in eFatigue.
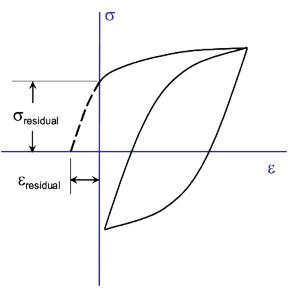
Residual stress is converted into a residual strain in the analysis to account for plastic deformation around the weld toe. Tensile residual stresses result in tensile residual strains..
Stress Concentration Factor
The stress concentration of a weld depends on the flank angle, θ, plate thickness, t, and local weld toe radius, r.
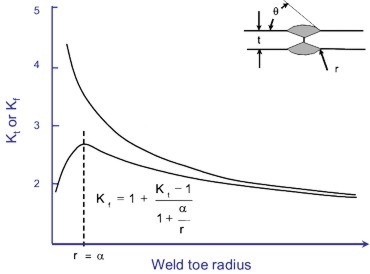
In a weld, the weld toe radius is variable along the length of the weld and can have any value. But small radii are less effective in fatigue than larger ones. As a result, there is a critical radius for fatigue that will result in the maximum fatigue notch factor, Kf. This critical radius is equal to the material parameter α in Peterson's equation.
Data from Mattos and Lawrence "Estimation of the Fatigue Crack Initiation Life in Welds using Low Cycle Fatigue Concepts" Fracture Control Program Report 19, 1975" was curve fit to obrtain this expression for Kf
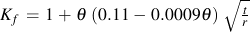
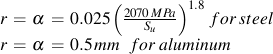
 日本語
日本語